زمان تخمینی مطالعه: 18 دقیقه 

الگوریتم‌های خوشه‌بندی (Clustering) الگوریتم‌هایی هستند که از طریق گروه‌بندی داده‌ها بر اساس شباهت یا الگوهای مشابه، داده‌ها را به خوشه‌های مجزا تقسیم می‌کنند. خوشه‌بندی یک روش بدون نظارت است، به این معنی که در این الگوریتم‌ها برچسب‌های کلاس موردنظر از قبل مشخص نیست و خوشه‌بندی بر اساس اطلاعات موجود در داده‌ها انجام می‌شود. امروزه، الگوریتم‌های مختلفی در ارتباط با خوشه‌بندی مورد استفاده قرار می‌گیرد که در این مقاله با مهم‌ترین الگوریتم‌ها آشنا خواهیم شد.

K-Means

این الگوریتم یکی از پرکاربردترین الگوریتم‌های خوشه‌بندی است. در این الگوریتم، داده‌ها به خوشه‌ها تقسیم می‌شوند به نحوی که هر داده به خوشه‌ای اختصاص پیدا کند که مرکز آن خوشه بهترین مطابقت را با داده‌ها داشته باشد. الگوریتم به صورت مرحله به مرحله اجرا می‌شود و در هر مرحله، مرکز هر خوشه به مرکز جدیدی به خوشه‌ای که مراکز خوشه‌ها به آن نزدیکتر باشند، به روزرسانی می‌شود. این فرایند تا زمانی ادامه می‌یابد که مراکز خوشه‌ها دیگر تغییر نکند. این مراحل به شرح زیر هستند.

1. مقداردهی اولیه: ابتدا، تعداد K مرکز خوشه (centroid) اولیه را به طور تصادفی انتخاب می‌کنیم. تعداد K توسط کاربر مشخص می‌شود و نشان‌دهنده تعداد خوشه‌های موردنظر است.
2. تخصیص خوشه: در این مرحله، به هر داده نزدیک‌ترین مرکز خوشه را اختصاص می‌دهیم. برای این منظور، می‌توان از معیار فاصله اقلیدسی بین داده‌ها و مراکز خوشه استفاده کرد. به عبارت دیگر، داده‌ها به خوشه‌ای اختصاص پیدا می‌کنند که فاصله آن‌ها تا مرکز آن خوشه کم‌ترین مقدار را داشته باشد.
3. به‌روزرسانی مراکز خوشه: در این مرحله، مراکز خوشه‌ها بر اساس میانگین داده‌هایی که به هر خوشه تخصیص یافته‌اند، به‌روزرسانی می‌شوند. به این صورت که برای هر خوشه، میانگین هر بعد از داده‌ها را محاسبه کرده و آن را به عنوان مرکز جدید خوشه در نظر می‌گیریم.
4. تکرار مراحل: مراحل دوم و سوم را تا جایی که مراکز خوشه دیگر تغییر نکنند تکرار می‌کنیم. به عبارت دیگر، خوشه‌بندی به صورت مکرر انجام می‌شود تا مراکز خوشه‌ها ثابت شوند و خوشه‌ها بهینه شوند.
5. مرحله پایانی: در نهایت، پس از اتمام تکرارها، خوشه‌بندی نهایی حاصل از الگوریتم K-Means به دست می‌آید که می‌توانیم داده‌ها را بر اساس خوشه‌هایی که به آن‌ها تخصیص یافته‌اند، مرتب کنیم.

الگوریتم K-Means یک الگوریتم خوشه‌بندی است که بر مبنای ایده تشکیل خوشه‌هایی از داده‌های مشابه به هم، داده‌ها را به گروه‌های مجزا تقسیم می‌کند. در این الگوریتم، تعداد K خوشه (که توسط کاربر مشخص می‌شود) از پیش تعیین می‌شود و میانگین داده‌ها در هر خوشه به عنوان مرکز خوشه در نظر گرفته می‌شود.

الگوریتم DBSCAN

این الگوریتم بر اساس چگالی نقاط و همسایگی آن‌ها خوشه‌بندی را انجام می‌دهد. داده‌هایی که در نزدیکی یکدیگر قرار دارند و چگالی کافی دارند، به عنوان یک خوشه شناخته می‌شوند. DBSCAN قادر است خوشه‌هایی با شکل‌ها و اندازه‌های متفاوت تشخیص دهد و داده‌هایی که از خوشه‌ها فاصله دارند را به عنوان داده‌های پراکنده (پرت) تعیین کند. DBSCAN قادر است به طور خودکار خوشه‌هایی با اشکال و اندازه‌های متفاوت تشخیص دهد و همچنین نقاطی که به هیچ خوشه‌ای تعلق ندارند را به عنوان نویز شناسایی کند. عملکرد الگوریتم DBSCAN به شرح زیر است:

1. انتخاب نقطه اولیه: یک نقطه را به عنوان نقطه انتخابی اولیه انتخاب می‌کنیم.
2. تشکیل خوشه: با استفاده از نقطه انتخابی اولیه، نقاطی که در محدوده فاصله (ε) قرار دارند و تعداد حداقل نقاطی (MinPts) را دارند، را به عنوان خوشه جدید تشخیص می‌دهیم. نقاطی که در محدوده فاصله ε قرار دارند، به عنوان همسایگان مستقیم در نظر گرفته می‌شوند.
3. گسترش خوشه: اگر یک نقطه در خوشه قبلی قرار داشته باشد، نقاطی که در محدوده فاصله ε قرار دارند و تعداد حداقل نقاطی را دارند، به خوشه موجود اضافه می‌شوند. این فرایند تا جایی ادامه می‌یابد که دیگر نقاطی به خوشه اضافه نشوند.
4. تشخیص نویز: نقاطی که تعداد همسایگان در محدوده فاصله ε کمتر از حداقل تعداد نقاط (MinPts) است، به عنوان نقاط نویز شناسایی می‌شوند و به هیچ خوشه‌ای تعلق ندارند.
5. مرحله پایانی: پس از اتمام تشکیل خوشه‌ها، خوشه‌های نهایی به همراه نقاط نویز بدست می‌آید و می‌توانیم داده‌ها را بر اساس خوشه‌هایی که به آن‌ها تعلق دارند، مرتب کنیم.

در الگوریتم DBSCAN، تعداد حداقل نقاط (MinPts) و فاصله حداکثر بین نقاط (ε) از پیش تعیین می‌شوند. MinPts نشان‌دهنده تعداد حداقل نقاطی است که باید در محدوده فاصله(ε) یکدیگر را داشته باشند تا یک خوشه تشکیل شود. ε نیز نشان‌دهنده فاصله حداکثر بین نقاط است که مورد استفاده قرار می‌گیرد تا تعیین کند که یک نقطه به یک خوشه تعلق دارد یا خیر. الگوریتم DBSCAN قابلیت شناسایی خوشه‌هایی با اشکال مختلف دارد و به طور خودکار تعداد خوشه‌ها را تشخیص می‌دهد. همچنین، DBSCAN قادر است با شناسایی نقاط نویز، داده‌هایی را که به هیچ خوشه‌ای تعلق ندارند، مشخص کند. این الگوریتم یکی از الگوریتم‌های خوشه‌بندی محبوب در حوزه داده‌کاوی و تحلیل داده است.

خوشه بندی انتشار وابستگی (Affinity Propagation)

این الگوریتم بر اساس شباهت نقاط با یکدیگر و ارسال پیغام‌ها بین نقاط برای تعیین نماینده‌ها اقدام به خوشه‌بندی می‌کند. به بیان دقیق‌ترف الگوریتم خوشه‌بندی Affinity Propagation یک الگوریتم خوشه‌بندی بدون نیاز به تعیین تعداد خوشه می‌باشد. این الگوریتم بر مبنای تکنیک affinity بین نقاط داده‌ها عمل می‌کند و به طور خودکار مراکز خوشه‌ها را تعیین می‌کند. عملکرد الگوریتم Affinity Propagation به شرح زیر است:

1. محاسبه شباهت: ابتدا برای هر نقطه از داده‌ها، شباهت آن نسبت به سایر نقاط محاسبه می‌شود. شباهت ممکن است بر اساس معیارهای مختلفی مانند فاصله اقلیدسی یا معیارهای دیگر تعیین شود.
2. به‌روزرسانی مقادیر انتشار تاثیر: در این مرحله، تاثیر نقاط بر یکدیگر به روزرسانی می‌شوند. هر نقطه به نقاط دیگر پیامی ارسال می‌کند که شامل شباهت آن نقطه با نقطه مقصد و مقدار انتشار تاثیر فعلی است.
3. به‌روزرسانی مقادیر مقصد: در این مرحله، مقادیر مقصد بر اساس پیام‌های دریافتی در مرحله قبلی به روزرسانی می‌شوند. مقادیر مقصد نشان‌دهنده میزان مطلوبیت یا تمایل هر نقطه برای انتخاب شدن به عنوان مرکز خوشه است.
4. تعیین مراکز خوشه: پس از به‌روزرسانی مقادیر انتشار تاثیر و مقادیر مقصد، برای هر نقطه تعیین می‌شود که آیا به عنوان مرکز خوشه خودش انتخاب شود یا خیر. نقاطی که مقدار مطلوبیت بیشتری دارند به عنوان مرکز خوشه انتخاب می‌شوند.
5. مرحله پایانی: در این مرحله، نقاط به خوشه‌ها تخصیص داده می‌شوند و هر نقطه به مرکز خوشه مناسب خود متصل می‌شود.

مزیت اصلی الگوریتم Affinity Propagation این است که به طور خودکار تعداد خوشه‌ها را تعیین می‌کند و نیازی به تعیین تعداد خوشه از قبل وجود ندارد. این الگوریتم قابلیت شناسایی خوشه‌های با اشکال و اندازه‌های متفاوت را دارد و معمولا در ارتباط با داده‌هایی با توزیع نامنظم و بدون فرضیات خاص استفاده می‌شود. همچنین، الگوریتم Affinity Propagation قادر است به طور همزمان مراکز خوشه‌ها را تعیین کند و به عنوان یک الگوریتم خوشه‌بندی مستحکم شناخته می‌شود. این الگوریتم در حوزه‌های گوناگونی مانند تحلیل تصویر، تحلیل متن، بیوانفورماتیک و سیستم‌های توصیه‌گر مورد استفاده قرار می‌گیرد.

خوشه بندی سلسله مراتبی (Hierarchical Clustering)

این الگوریتم داده‌ها را در یک سلسله‌مراتبی از خوشه‌ها قرار می‌دهد. ابتدا، هر داده به عنوان یک خوشه مجزا در نظر گرفته می‌شود و سپس خوشه‌ها به تدریج با یکدیگر ادغام می‌شوند تا یک ساختار سلسله‌مراتبی از خوشه‌ها به وجود آید. این ساختار سلسله‌مراتبی می‌تواند به صورت گراف درختی نمایش داده شود و در نهایت، با توجه به نیاز، تعداد موردنظری از خوشه‌ها برای استفاده انتخاب می‌شود. این روش به شکل درخت‌وار ارتباط بین خوشه‌ها را نمایش می‌دهد و می‌تواند به صورت تجزیه‌پذیر یا غیرتجزیه‌پذیر استفاده شود. فرایند کار خوشه‌بندی سلسله‌مراتبی به شرح زیر است.

1. ساخت خوشه‌های اولیه: هر نقطه ابتدا به عنوان یک خوشه جداگانه در نظر گرفته می‌شود.
2. محاسبه ماتریس شباهت: یک ماتریس شباهت بین هر دو خوشه محاسبه می‌شود. معیارهای مختلفی برای محاسبه شباهت می‌توانند استفاده شوند، مانند فاصله اقلیدسی یا ضریب همبستگی.
3. ادغام خوشه‌ها: دو خوشه که بیشترین شباهت را دارند، با یکدیگر ادغام می‌شوند و یک خوشه جدید تشکیل می‌دهند.
4. به‌روزرسانی ماتریس شباهت: ماتریس شباهت به‌روزرسانی می‌شود تا شامل خوشه جدید ادغام شده باشد.
5. تکرار مراحل: مراحل سوم و چهارم تا جایی که یک خوشه نهایی به دست آید، تکرار می‌شوند. این روند ادامه می‌یابد تا همه نقاط به یک خوشه نهایی تعلق گیرند.

در حین ادغام خوشه‌ها، می‌توان از روش‌های مختلفی برای محاسبه فاصله بین خوشه‌ها استفاده کرد. دو روش معمول برای ادغام خوشه‌ها وجود دارد. روش ادغام کامل (Complete Linkage) که در این روش، فاصله بیشترین شباهت بین دو خوشه به عنوان شباهت خوشه‌ها در نظر گرفته می‌شود. روش ادغام میانگین (Average Linkage) که میانگین فاصله شباهت بین تمام نقاط دو خوشه به عنوان شباهت خوشه‌ها در نظر گرفته می‌شود.

خوشه بندی مخفی مارکوف (Hidden Markov Clustering)

 این الگوریتم بر اساس مدل مخفی مارکوف (Hidden Markov Model) عمل می‌کند و برای خوشه‌بندی داده‌ها از ترکیب شباهت گراف (Graph Similarity) و تحلیل مخفی مارکوف استفاده می‌کند. در این الگوریتم، گرافی که نماینده‌ داده‌ها است با استفاده از مدل مخفی مارکوف تشکیل می‌شود و خوشه‌بندی انجام می‌شود.

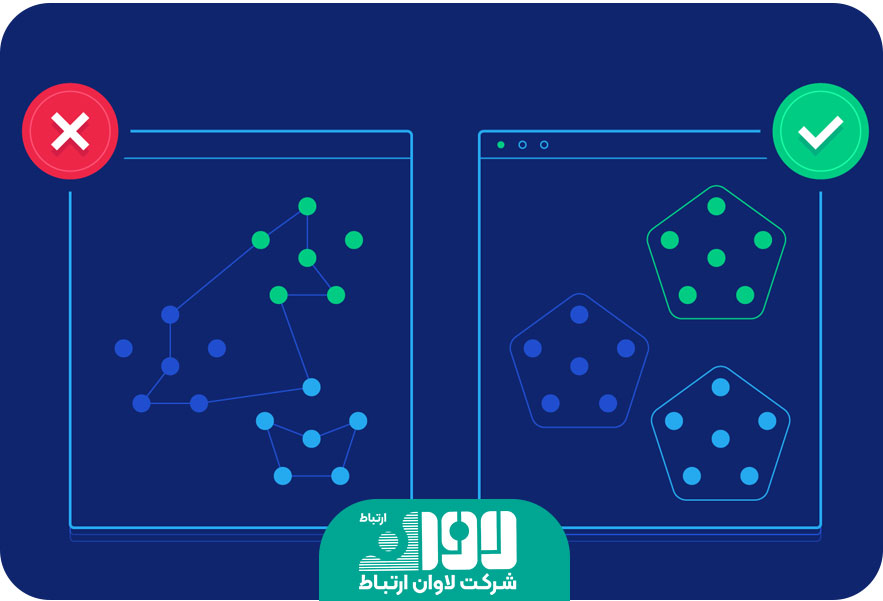
خوشه بندی مبتنی بر روش های احتمالی (Probabilistic Clustering)

این دسته از الگوریتم‌ها بر اساس مدل‌های احتمالی مانند مدل مخلوط گاوسی (Gaussian Mixture Model) عمل می‌کنند. این الگوریتم‌ها فرض می‌کنند که داده‌ها از توزیع‌های احتمالی مختلفی نشات می‌گیرند و سعی می‌کنند توزیع‌های احتمالی که بهترین توصیفی برای داده‌ها هستند را تخمین بزنند. سپس، با استفاده از این توزیع‌های احتمالی، داده‌ها را به خوشه‌های مختلف تقسیم می‌کنند. در خوشه‌بندی مبتنی بر روش‌های احتمالی، فرضیاتی در مورد توزیع احتمالی داده‌ها وجود دارد. معمولا از مدل‌های احتمالی مانند مدل‌های توزیع گاوسی مختلف، مدل‌های مخلوط توزیع‌ها (mixture models)، مدل‌های بیزی و غیره استفاده می‌شود. روش‌های خوشه‌بندی مبتنی بر روش‌های احتمالی عموما به دنبال یافتن پارامترهای مناسب مدل احتمالی هستند که داده‌ها را به خوشه‌های مختلف توزیع می‌دهند. این پارامترها می‌توانند شامل مرکز خوشه‌ها، ماتریس‌های کوواریانس، وزن‌های خوشه‌ها و احتمال تعلق داده‌ها به هر خوشه باشند. روش‌های خوشه‌بندی مبتنی بر روش‌های احتمالی معمولا با استفاده از الگوریتم‌های بهینه‌سازی مثل امیدریاضی (Expectation-Maximization) یا الگوریتم انتقال پس‌پیوسته (Continuous-Valued Viterbi Algorithm) برای یافتن پارامترهای بهینه توزیع احتمالی و تخصیص داده‌ها به خوشه‌ها استفاده می‌کنند. در این روش‌ها، پس از آموزش مدل احتمالی با استفاده از داده‌های آموزشی، می‌توان از مدل برای پیش‌بینی تخصیص خوشه‌ها به داده‌های جدید استفاده کرد. مزیت اصلی خوشه‌بندی مبتنی بر روش‌های احتمالی، این است که معمولا مدل‌های احتمالی قادر به مدل‌سازی توزیع نامعلوم داده‌ها هستند و توانایی کشف ساختارهای پنهان و پیچیده در داده‌ها را دارند.

الگوریتم خوشه بندی مخلوط گاوسی 

الگوریتم خوشه‌بندی ترکیبی گاوسی (Gaussian Mixture Clustering) یک الگوریتم خوشه‌بندی است که بر پایه مدل‌های مخلوط توزیع‌های گاوسی عمل می‌کند. این الگوریتم می‌تواند داده‌ها را به خوشه‌های مختلف توزیع دهد و هر خوشه را با استفاده از یک توزیع گاوسی مشخص کند. مراحل اصلی الگوریتم خوشه‌بندی مخلوط گاوسی به شرح زیر است.

1. مقداردهی اولیه: مقادیر اولیه برای پارامترهای مدل مخلوط گاوسی انتخاب می‌شود. این پارامترها شامل تعداد خوشه‌ها، میانگین، ماتریس کوواریانس و وزن‌های خوشه‌ها است.
2. محاسبه احتمال تعلق به هر خوشه: بر اساس پارامترهای فعلی مدل، احتمال تعلق هر نقطه داده به هر خوشه محاسبه می‌شود. این احتمالات با استفاده از تابع چگالی احتمال گاوسی (Gaussian Probability Density Function) محاسبه می‌شوند.
3. تخصیص بهترین خوشه: هر نقطه داده به خوشه‌ای تخصیص می‌یابد که احتمال تعلق آن به آن خوشه بیشترین مقدار را دارد.
4. به‌روزرسانی پارامترها: پس از تخصیص نقاط داده به خوشه‌ها، پارامترهای مدل (میانگین، ماتریس کوواریانس و وزن‌های خوشه‌ها) با استفاده از روش بهینه‌سازی مثل الگوریتم امیدریاضی (Expectation-Maximization) به‌روزرسانی می‌شوند. در مرحله امید، احتمال تعلق داده‌ها به خوشه‌ها محاسبه می‌شود و در مرحله بیشینه‌سازی، پارامترهای مدل به صورتی به‌روزرسانی می‌شوند که احتمال تعلق داده‌ها به خوشه‌ها بیشینه شود.
5. تکرار مراحل: مراحل 2 تا 4 تا زمانی که معیار همگرایی مشخص شده (مانند تغییرات کوچک در پارامترها یا تعداد تکرارها) برآورده شود تکرار می‌شوند.
6. اتمام الگوریتم: الگوریتم پس از رسیدن به شرایط توقف مشخص شده متوقف می‌شود و خوشه‌بندی نهایی را تولید می‌کند.

با تکرار مراحل 2 تا 4، الگوریتم بهبود می‌یابد. این روند تا زمانی ادامه می‌یابد که مدل به یک حد همگرایی برسد و پارامترها ثابت شوند. در نهایت، خوشه‌بندی نهایی بر اساس تخصیص نقاط به خوشه‌ها بدست می‌آید. نقاطی که به یک خوشه تخصیص پیدا کرده‌اند، در یک خوشه قرار می‌گیرند و نقاطی که به خوشه‌های مختلف تخصیص داده شده‌اند، در خوشه‌های مختلف قرار می‌گیرند. الگوریتم خوشه‌بندی مخلوط گاوسی بسیار رایج و قدرتمند است و می‌توانند در مواردی که داده‌ها از توزیع‌های مختلف گاوسی تشکیل شده‌اند، عملکرد بسیار خوبی داشته باشد. همچنین، این الگوریتم قابلیت استفاده در مسائلی را دارد که داده‌ها ساختار پیچیده‌ای دارند.

الگوریتم خوشه بندی BIRCH

الگوریتم خوشه‌بندی BIRCH سرنام (Balanced Iterative Reducing and Clustering using Hierarchies) یک الگوریتم خوشه‌بندی سلسله مراتبی و متوازن است که برای پردازش و خوشه‌بندی حجم بالای داده‌ها طراحی شده است. این الگوریتم به منظور کاهش پیچیدگی محاسباتی مراحل تجزیه و تحلیل داده‌ها را در یک سلسله مراتبی انجام می‌دهد تا به خوشه‌بندی نهایی برسد. عملکرد الگوریتم خوشه‌بندی BIRCH به شرح زیر است.

1. ساختار سلسله مراتبی (Clustering Feature): در این مرحله، یک ساختار سلسله مراتبی CF برای نگهداری اطلاعات خوشه‌بندی ساخته می‌شود. این ساختار شامل سه مقدار است: نماینده خوشه (cluster representative)، تعداد نقاط در هر خوشه و مرکزیت خوشه (cluster centroid) است. این ساختار برای حفظ خلاصه‌ای از داده‌ها و انجام محاسبات سریع‌تر استفاده می‌شود.
2. ادغام خوشه‌ها: در این مرحله، خوشه‌ها به صورت متوازن با هم ادغام می‌شوند. برای ادغام خوشه‌ها، مراحل زیر انجام می‌شود:

   – انتخاب دو خوشه نزدیک‌ترین به هم بر اساس مرکزیت خوشه.

   – ادغام دو خوشه با استفاده از روشی مشخص (ادغام میانگین وزنی).

   – به‌روزرسانی ساختار CF بر اساس ادغام خوشه‌ها.

3. تقسیم خوشه‌ها: اگر ساختار CF بزرگ‌تر از حد آستانه‌ای تعیین شده باشد، یعنی تعداد خوشه‌ها بیشتر از یک حد آستانه است، آنگاه خوشه‌ها تقسیم می‌شوند. این تقسیم بر اساس تابعی از فاصله مرکزیت خوشه‌ها انجام می‌شود. در نتیجه، تعداد خوشه‌ها افزایش می‌یابد.
4. خوشه‌بندی نهایی: پس از تقسیم و ادغام مراحل قبلی، خوشه‌بندی نهایی بر اساس ساختار CF به‌دست می‌آید. هر خوشه به صورت نماینده خوشه توسط مرکزیت خوشه و تعداد نقاط در آن خوشه تعیین می‌شود.

الگوریتم BIRCH به دلیل استفاده از ساختار سلسله مراتبی CF و متوازن بودن برای داده‌های بزرگ به خوبی مقیاس‌پذیر است. همچنین، از آنجایی که خلاصه‌ای از داده‌ها را استفاده می‌کند، به صورت موازی و با سرعت بالا قابل اجرا است. با استفاده از الگوریتم BIRCH می‌توانید داده‌های خود را به خوشه‌های مشابه تقسیم کنید و درک بهتری از ساختار داده‌ها و الگوهای موجود در آن‌ها به‌دست آورید.

الگوریتم خوشه بندی OPTICS

الگوریتم خوشه‌بندی OPTICS سرنام (Ordering Points To Identify the Clustering Structure) یک الگوریتم خوشه‌بندی مبتنی بر ترتیب است که برای تشخیص ساختار خوشه‌ها در داده‌ها استفاده می‌شود. OPTICS در واقع یک گسترش از الگوریتم DBSCAN است که مجازی توابع فاصله برای تعیین نقاط مجاورت و شعاع خوشه‌ها را استفاده می‌کند. عملکرد الگوریتم خوشه‌بندی OPTICS به شرح زیر است.

1. محاسبه همسایگی: در این مرحله، برای هر نقطه‌ای در مجموعه داده، فاصله آن با نقاط دیگر محاسبه می‌شود. این فاصله می‌تواند بر اساس معیارهای مختلفی مانند فاصله اقلیدسی محاسبه شود. سپس بر اساس فاصله‌ها، نقاطی که در شعاع یکدیگر قرار دارند، به عنوان همسایگان هر نقطه شناخته می‌شوند.
2. محاسبه ترتیب: در این مرحله، ترتیب (Ordering) برای هر نقطه محاسبه می‌شود. ترتیب به عنوان یک معیار برای تشخیص ساختار خوشه‌ها استفاده می‌شود. ترتیب نشان می‌دهد که هر نقطه چقدر درون یک خوشه قرار دارد و چقدر از خوشه‌های دیگر فاصله دارد. نقاطی که درون یک خوشه قرار دارند، ترتیب بزرگ‌تری دارند و نقاطی که دورترین فاصله را دارند، ترتیب کوچک‌تری دارند.
3. تشکیل خوشه‌ها: در این مرحله، خوشه‌ها بر اساس ترتیب مشخص می‌شوند. با استفاده از ترتیب، می‌توانیم نقاطی که درون یک خوشه قرار دارند را تشخیص دهیم. همچنین، با مشاهده تغییرات در ترتیب، می‌توانیم مرزهای بین خوشه‌ها را شناسایی کنیم.
4. استخراج خوشه‌ها: در این مرحله، با استفاده از ترتیب و شعاع‌های خوشه‌ها، خوشه‌ها استخراج می‌شوند. با تعیین نقاط مرزی برای هر خوشه، می‌توانیم نقاط را به خوشه‌های مختلف تقسیم کنیم.

الگوریتم OPTICS از مزایایی مانند قابلیت تشخیص خوشه‌های با اشکال نامتناهی و تنوع شعاع خوشه‌ها برخوردار است. علاوه بر این، این الگوریتم از بروز مشکل خوشه‌بندی براساس مرجعیت (Reference Clustering) وابسته به پارامترها جلوگیری می‌کند و به طور خودکار تعداد و شکل خوشه‌ها را تشخیص می‌دهد.

الگوریتم خوشه بندی طیفی را شرح بده

الگوریتم خوشه‌بندی طیفی (Spectral Clustering) بر اساس اطلاعات مربوط به طیف یا ویژگی‌های مرتبط با داده‌ها عمل می‌کند. این الگوریتم برای خوشه‌بندی داده‌ها با ساختار غیر خطی و پیچیده مناسب است. عملکرد الگوریتم خوشه‌بندی طیفی به شرح زیر است.

1. ساخت ماتریس شباهت: در این مرحله، یک ماتریس شباهت برای داده‌ها ساخته می‌شود. معمولا از معیارهای شباهتی مانند معیار اقلیدسی یا معیار شباهت گاوسی (Gaussian similarity) استفاده می‌شود. این ماتریس نمایان‌گر میزان شباهت بین هر زوج داده است، به طوری که داده‌های مشابه دارای مقادیر بزرگ‌تری در ماتریس شباهت هستند.
2. تجزیه مقادیر ویژه: در این مرحله، ماتریس شباهت، فرآیند تجزیه مقادیر ویژه را انجام می‌دهد تا ویژگی‌های مهم و معنی‌دار طیفی آن‌را استخراج شوند. با استفاده از تجزیه مقادیر ویژه، می‌توان اطلاعات ساختاری و مهم داده‌ها را استخراج کرده و برای خوشه‌بندی استفاده کرد.
3. انجام خوشه‌بندی: پس از استخراج ویژگی‌های مهم طیفی، می‌توان از روش‌های خوشه‌بندی معمول مانند خوشه‌بندی k-means بر روی این ویژگی‌ها استفاده کرد. با استفاده از الگوریتم خوشه‌بندی، داده‌ها به گروه‌های مختلف با توجه به ویژگی‌های مهم و طیفی تقسیم می‌شوند.
4. تفسیر خوشه‌ها: پس از خوشه‌بندی، می‌توان اطلاعاتی درباره خوشه‌ها و روابط بین آن‌ها استخراج کرد و آن‌ها را تفسیر کرد. ممکن است نیاز به روش‌های بصری‌سازی مانند نمودارهای داده‌ها (مانند نمودار پراکندگی) یا تحلیل مرتبط دیگر باشد تا خوشه‌ها و روابط بین آن‌ها به طور دقیق‌تر مورد بررسی قرار بگیرند.

الگوریتم خوشه‌بندی طیفی به عنوان یک روش قدرتمند برای برای تشخیص و خوشه‌بندی داده‌هایی با ساختار غیر خطی و پیچیده مفید است. با استفاده از طیف و ویژگی‌های طیفی، الگوریتم قادر است به خوشه‌بندی داده‌ها در فضای ویژگی‌های مهم ترکیبی دست پیدا کند.

کاربرد الگوریتم های خوشه بندی

الگوریتم‌های خوشه‌بندی کاربردهای گسترده‌ای در حوزه‌های مختلف دارند. اولین مورد تحلیل الگو است. الگوریتم‌های خوشه‌بندی به ما کمک می‌کنند تا الگوها و ساختارهای موجود در داده‌ها را شناسایی کنیم. با تشخیص و خوشه‌بندی الگوها، می‌توانیم درک بهتری از داده‌ها و ارتباطات بین آن‌ها پیدا کنیم. این کاربرد در زمینه‌هایی مانند تحلیل اجتماعی، تحلیل ترافیک، تحلیل بازار و غیره مورد استفاده قرار می‌گیرد. الگوریتم‌های خوشه‌بندی در تحلیل تصاویر و پردازش تصویر بسیار مفید هستند. با استفاده از خوشه‌بندی، می‌توانیم تصاویر را بر اساس ویژگی‌های مشابه به گروه‌های مختلف تقسیم کنیم. این کاربرد در زمینه‌هایی مانند تشخیص الگو، دسته‌بندی تصاویر و غیره استفاده می‌شود.

الگوریتم‌های خوشه‌بندی به خصوص در تجزیه و تحلیل داده‌های بزرگ و پیچیده بسیار کارآمد هستند. این الگوریتم‌ها به ما اجازه می‌دهند داده‌ها را به خوشه‌های کوچک‌تر و مدل‌پذیر تقسیم کنیم که برای تحلیل و فهم بهتر داده‌ها الزامی است. این کاربرد در زمینه‌هایی مانند تحلیل داده‌های اینترنتی، تحلیل متن، تحلیل تاریخچه و تحلیل ترافیک شبکه مورد استفاده قرار می‌گیرد. الگوریتم‌های خوشه‌بندی می‌توانند به ما در طبقه‌بندی داده‌ها و تشخیص الگو کمک کنند. با تشخیص خوشه‌های مختلف، می‌توانیم داده‌ها را به دسته‌های مشابه تقسیم کرده و الگوهای مشترک در هر دسته را شناسایی کنیم. این کاربرد در زمینه‌هایی مانند طبقه‌بندی متن، تشخیص الگوها در حوزه‌های پزشکی، تشخیص تقلب در سیستم‌های مالی و تشخیص همبستگی در شبکه‌های اجتماعی مورد استفاده قرار می‌گیرد.

با استفاده از الگوریتم‌های خوشه‌بندی، می‌توانیم داده‌ها را به زیرمجموعه‌های کوچکتر و یکنواخت تقسیم کنیم تا تحلیل و پردازش آن‌ها ساده‌تر و کارآمدتر شود. این کاربرد در زمینه‌هایی مانند تحلیل داده‌های مالی، تحلیل بازار، تحلیل مشتریان و تحلیل عملکرد سیستم‌ها استفاده می‌شود. در نهایت الگوریتم‌های خوشه‌بندی می‌توانند در سیستم‌های توصیه‌گر مورد استفاده قرار بگیرند. با تجزیه عملکرد کاربران یا محصولات به خوشه‌های مشابه، می‌توانیم بهترین پیشنهادات را برای کاربران با توجه به سلایق و نیازهایشان ارائه دهیم. این کاربرد در زمینه‌هایی مانند توصیه خرید، توصیه موسیقی و مقالات علمی استفاده می‌شود.

بخوانید: اتوماسیون در دنیای یادگیری ماشین: ظهور AutoML