رگرسیون لجستیک

زمان تخمینی مطالعه: 18 دقیقه 

رگرسیون در آمار و علوم داده یک روش تحلیلی است که برای بررسی رابطه بین یک متغیر وابسته (متغیر پاسخ) و یک یا چند متغیر مستقل (متغیرهای توضیحی) استفاده می‌شود. هدف اصلی رگرسیون، پیش‌بینی یا تخمین مقدار متغیر پاسخ بر اساس مقادیر متغیرهای توضیحی است. در رگرسیون، یک مدل ریاضی بر اساس داده‌های موجود ساخته می‌شود تا رابطه بین متغیرهای وابسته و مستقل را توصیف کند. این مدل به عنوان یک تابع رگرسیون که ممکن است خطی یا غیرخطی باشد، نمایش داده می‌شود. با استفاده از این مدل، می‌توان مقدار متغیر پاسخ را برای مقادیر جدید متغیرهای توضیحی پیش‌بینی کرد.

یکی از مدل‌های رگرسیون معروف، رگرسیون خطی است که ماهیت مستقیم دارد، اما روش‌های رگرسیون غیرخطی مانند رگرسیون لجستیک و رگرسیون چندجمله‌ای نیز وجود دارند که مدل‌های پیچیده‌تری را برای توصیف رابطه بین متغیرها ارائه می‌دهند. رگرسیون به عنوان یکی از ابزارهای اصلی تحلیل داده، در حوزه‌های مختلفی مانند علوم اجتماعی، اقتصاد، پزشکی، مهندسی و غیره استفاده می‌شود.

رگرسیون خطی چیست

رگرسیون خطی یک روش آماری است که برای بررسی رابطه بین یک متغیر وابسته (متغیر پاسخ) و یک یا چند متغیر مستقل (متغیرهای پیش‌بین) استفاده می‌شود. در رگرسیون خطی، فرضیه این است که رابطه بین متغیرهای وابسته و مستقل را می‌توان با یک خط ریاضی ساده توصیف کرد. در رگرسیون خطی، سعی می‌شود خطی‌ترین رابطه ممکن بین متغیرهای وابسته و مستقل پیدا شود. به این معنی که مستقیم‌ترین خطی که می‌تواند به نمونه‌های داده نزدیک شود و خطاهای پیش‌بینی را کمینه کند، تعیین می‌شود. در رگرسیون خطی، از مدل خطی استفاده می‌شود که شامل یک عبارت ثابت (عبارت تداوم) و ضرایب (پارامترها) برای هر متغیر مستقل است. مدل رگرسیون خطی به شکل زیر نشان داده می‌شود:

Y = β₀ + β₁X₁ + β₂X₂ + … + βₚXₚ + ε

در این مدل، Y نشان دهنده متغیر وابسته است و X₁ تا Xₚ متغیرهای مستقل هستند. β₀ تداوم مدل را نشان می‌دهد و β₁ تا βₚ ضرایب مربوط به متغیرهای مستقل هستند. ε نشان دهنده خطاهای تصادفی است. برای تخمین پارامترها و ارزیابی مدل رگرسیون خطی، از روش کمترین مربعات استفاده می‌شود که با رابطه‌ای ریاضی، پارامترها را به‌دست می‌آورد که خطاهای مربعاتی را کمینه کند. رگرسیون خطی معمولا برای پیش‌بینی و تحلیل رابطه علیتی بین متغیرها استفاده می‌شود.

رگرسیون لجستیک

رگرسیون لجستیک (Logistic Regression) یک روش آماری است که برای پیش‌بینی و تحلیل رابطه بین یک متغیر وابسته و یک یا چند متغیر مستقل استفاده می‌شود. رگرسیون لجستیک به عنوان یک روش تخمین مدل احتمال استفاده می‌شود و معمولا در مسایل طبقه‌بندی استفاده می‌شود. در رگرسیون لجستیک، متغیر وابسته یا متغیر پاسخ یک متغیر دودویی (مثلا بله/خیر، 0/1) است. این روش به ما اجازه می‌دهد تا احتمال یک رویداد یا دسته‌بندی را بر اساس متغیرهای مستقل پیش‌بینی کنیم. به عبارت دیگر، رگرسیون لجستیک به ما اجازه می‌دهد تا احتمال تعلق یا عدم تعلق به یک دسته را بر اساس متغیرهای مستقل تخمین بزنیم. مدل رگرسیون لجستیک اغلب با استفاده از تابع لجستیک (یا تابع سیگمویید) برای تبدیل خروجی به مقادیر احتمالی بین 0 و 1 کار می‌کند. تابع لجستیک به شکل زیر تعریف می‌شود:

P(Y=1|X) = 1 / (1 + e^-(β₀ + β₁X₁ + β₂X₂ + … + βₚXₚ))

در این مدل، P(Y=1|X) نشان‌دهنده احتمال تعلق به دسته یک است و X₁ تا Xₚ متغیرهای مستقل هستند. β₀ تداوم مدل را نشان می‌دهد و β₁ تا βₚ ضرایب مربوط به متغیرهای مستقل هستند. برای تخمین پارامترها و ارزیابی مدل رگرسیون لجستیک نیز از روش کمترین مربعات یا روش ماکزیمم درست‌نمایی استفاده می‌شود. رگرسیون لجستیک معمولا برای مسایل طبقه‌بندی به کار می‌رود مانند پیش‌بینی احتمال بروز یک بیماری بر اساس عوامل ریسک، تحلیل سلسله‌مراتبی در تحقیقات پزشکی، تشخیص احتمال رفتار خرید مشتریان و سایر موارد مشابه.

رگرسیون چندجمله ای

رگرسیون چندجمله‌ای (Polynomial Regression) یک روش دیگر آماری است که برای بررسی رابطه بین یک متغیر وابسته و یک یا چند متغیر مستقل استفاده می‌شود، اما بر عکس رگرسیون خطی، از توابع چندجمله‌ای برای توصیف رابطه استفاده می‌کند. در رگرسیون چندجمله‌ای، فرضیه این است که رابطه بین متغیرهای وابسته و مستقل را می‌توان با یک تابع چندجمله‌ای توصیف کرد. به عنوان مثال، اگر متغیرهای مستقل را با X₁، X₂ و X₃ نشان دهیم، یک مدل رگرسیون چندجمله‌ای درجه دو به صورت زیر تعریف می‌شود:

Y = β₀ + β₁X₁ + β₂X₂ + β₃X₃ + β₄X₁² + β₅X₂² + β₆X₃² + β₇X₁X₂ + β₈X₁X₃ + β₉X₂X₃

در این مدل، β₀ تداوم مدل را نشان می‌دهد و β₁ تا β₉ ضرایب مربوط به متغیرهای مستقل هستند. همچنین، X₁²، X₂² و X₃² نمایانگر جمله‌های چندجمله‌ای درجه دو هستند، و X₁X₂، X₁X₃ و X₂X₃ نمایانگر جمله‌های ترکیبی متقابل هستند. رگرسیون چندجمله‌ای به ما اجازه می‌دهد تا روابط غیرخطی و پیچیده‌تری را نسبت به رگرسیون خطی مدل‌سازی کنیم. با افزایش درجه چندجمله‌ای، می‌توانیم روابط بیشتری را توصیف کنیم، اما باید مراقب برازش بیش‌ازحد داده‌ها باشیم تا به پدیده‌ای به نام بیش‌برازش (overfitting) گرفتار نشویم. رگرسیون چندجمله‌ای معمولا در مواردی استفاده می‌شود که رابطه بین متغیرها به صورت منحنی یا غیرخطی است، مانند تحلیل داده‌های علوم طبیعی، مهندسی، اقتصاد و سایر حوزه‌های تحقیقاتی که روابط پیچیده‌تری دارند.

تحلیل رگرسیون

همان‌گونه که اشاره کردیم تحلیل رگرسیون شامل چند مرحله است که برای بررسی رابطه بین متغیرهای وابسته و مستقل استفاده می‌شود. مراحل اصلی تحلیل رگرسیون به این صورت است که ابتدا فرآیند جمع‌آوری داده‌ها انجام می‌شود تا داده‌های مربوط به متغیرهای وابسته و مستقل جمع‌آوری شوند. این داده‌ها می‌توانند به صورت آزمایشی یا مشاهده‌ای دریافت شوند. مرحله بعد نوبت به تهیه نمودارها می‌رسد.  معمولا ابتدای تحلیل رگرسیون، نمودارهای متغیرهای وابسته و مستقل رسم می‌شوند. این نمودارها می‌توانند به شناخت الگوها و رابطه‌های میان متغیرها کمک کنند. هنگامی که نمودارها آماده شدند باید به سراغ انتخاب مدل رگرسیون برویم. بر اساس خصوصیات داده‌ها و هدف تحلیل، مدل رگرسیون مناسب برای استفاده را انتخاب می‌کنیم. در این مرحله رگرسیون خطی یا رگرسیون غیرخطی مانند رگرسیون لجستیک، رگرسیون چندجمله‌ای و غیره می‌توانند انتخاب شوند.

مرحله بعد نوبت به تخمین پارامترها می‌رسد. با استفاده از داده‌ها، پارامترهای مدل رگرسیون، مانند ضرایب را تخمین بزنید. این مرحله ممکن است با استفاده از روش‌های استنتاجی مانند روش کمترین مربعات صورت بگیرد. هنگامی که فرآیند تخمین پارامترها به پایان رسید نوبت به ارزیابی مدل می‌رسد. بررسی صحت و کارایی مدل رگرسیون بسیار مهم است. در این مرحله از روش‌های ارزیابی مانند رگرسیون معکوس، ضریب تعیین (R-squared) و تحلیل واریانس (ANOVA) استفاده می‌شود. هنگامی که مدل در دنیای واقعی پیاده‌سازی شد باید نتایج تحلیل رگرسیون تفسیر شده و بررسی شوند که متغیرهای مستقل تا چه اندازه بر متغیر وابسته تاثیردارند دارند و آیا رابطه آماری معناداری وجود دارد یا خیر. لازم به توضیح است که تحلیل رگرسیون پیچیده است و نیاز به درک مناسب از مباحث آمار و ریاضیات دارد.

در چه مواردی از تحلیل رگرسیون استفاده می‌شود؟

تحلیل رگرسیون در موارد مختلفی انجام می‌شود. اولین مورد پیش‌بینی است. ما از تحلیل رگرسیون برای پیش‌بینی مقادیر یک متغیر وابسته بر اساس متغیرهای مستقل استفاده می‌کنیم. به طور مثال، می‌توان از رگرسیون برای پیش‌بینی قیمت یک ملک بر اساس متغیرهایی مانند متراژ، تعداد اتاق‌ها و موقعیت جغرافیایی استفاده کرد. تحلیل رگرسیون می‌تواند برای بررسی تاثیر متغیرهای مستقل بر یک متغیر وابسته استفاده شود. این تحلیل می‌تواند رابطه‌های علیتی و ارتباطات آماری بین متغیرها را مشخص کند. به عنوان مثال، می‌توان از رگرسیون برای بررسی تاثیر سن، جنسیت، سابقه خانوادگی و سطح تحصیلات بر درآمد یک فرد استفاده کرد. در برخی موارد، تحلیل رگرسیون می‌تواند برای کنترل تاثیر متغیرهای مشترک بین دو متغیر استفاده شود. به عنوان مثال، می‌توان از رگرسیون برای بررسی تاثیر تمرین و تغذیه بر وزن بدن یک شخص با در نظر گرفتن سن او استفاده کرد.

همچنین، تحلیل رگرسیون می‌تواند به عنوان ابزاری برای تفسیر نتایج و بررسی اهمیت متغیرها در یک مدل استفاده شود. با تحلیل ضرایب رگرسیون، می‌توان مشخص کنید که هر متغیر مستقل به چه اندازه بر متغیر وابسته تاثیرگذار است.  همچنین، به منظور تصحیح خطاهای پیش‌بینی نیز استفاده می‌شود. می‌توان با استفاده از تحلیل رگرسیون خطاها را کاهش داد. با تحلیل خطاها، می‌توان مشخص کرد آیا مدل رگرسیون به طور قابل قبولی پیش‌بینی می‌کند یا خیر. در کل، تحلیل رگرسیون یک ابزار قدرتمند در تحلیل داده‌ها است که در موارد پیش‌بینی، تحلیل عوامل موثر، کنترل متغیرهای مشترک، تحلیل تفسیری و تصحیح خطاهای پیش‌بینی کاربرد دارد.

گرادیان کاهشی

گرادیان کاهشی (Gradient Descent) یک الگوریتم بهینه‌سازی است که در بسیاری از مسایل یادگیری ماشین و رگرسیون خطی استفاده می‌شود. هدف اصلی این الگوریتم، کمینه کردن تابع هدف (معمولا تابع خطا) با بهبود پارامترهای مدل است. فرض کنید می‌خواهیم یک تابع هدف J(w) را کمینه کنیم که w برداری از پارامترهای مدل است. الگوریتم گرادیان کاهشی به صورت تکراری پارامترها را به طور متوالی به سمت معکوس گرادیان تابع هدف حرکت می‌دهد تا به نقطه‌ای که گرادیان صفر می‌شود (یا به نقطه کمینه تابع هدف نزدیک می‌شود) برسد. عملکرد گرادیان کاهشی به این صورت است. ابتدا باید مقادیر اولیه برای پارامترهای مدل را تعیین کنید. در هر مرحله، باید گرادیان تابع هدف نسبت به پارامترها را محاسبه کنید. این عملیات معمولا با استفاده از قاعده زنجیره‌ای (chain rule) در محاسبه مشتقات جزیی تابع هدف نسبت به پارامترها انجام می‌شود. با استفاده از گرادیان محاسبه شده، پارامترها را به صورت معکوس گرادیان به‌روزرسانی می‌کنیم. این عملیات به صورت مکرر تکرار می‌شود تا به یک شرایط همگرایی برسید.

در ادامه بررسی می‌کنیم که آیا به شرایط توقف موردنظر رسیده‌ایم یا خیر. این شرایط می‌توانند مواردی مثل تعداد مشخصی تکرار، دست‌یابی به مقدار معینی برای تابع هدف یا تغییر کمتر از یک آستانه مشخص در پارامترها باشد. مرحل فوق به غیر از تعیین مقدار اولیه را تکرار می‌کنیم تا نقطه توقف برسیم. در صورتی که به چنین نقطه‌ای دست پیدا نکنیم باید پارامترها را به‌روزرسانی کرده و به مرحله محاسبه گرادیان بازگردیم. لازم به توضیح است که عملکرد گرادیان کاهشی به شدت وابسته به انتخاب نرخ یادگیری (learning rate) است. انتخاب نرخ یادگیری مناسب برای مسایل مختلف بسیار مهم است. نرخ یادگیری باید به گونه‌ای انتخاب شود که الگوریتم به سمت نقطه کمینه هدایت شود، اما در عین حال نرخ یادگیری بیشتر از حد می‌تواند باعث پیچیدگی و عدم همگرایی به نقطه کمینه شود. همچنین، نرخ یادگیری کمتر از حد می‌تواند باعث کند شدن فرایند همگرایی شود. انتخاب نرخ یادگیری مناسب یک فرایند آزمون و خطا است و ممکن است نیاز به تنظیمات متعدد و آزمون‌های متعدد داشته باشد.

همچنین، گرادیان کاهشی بهینه (Optimized Gradient Descent) نیز وجود دارد که تغییراتی بر روی الگوریتم گرادیان کاهشی اصلی اعمال می‌کند تا سرعت و کارایی الگوریتم را بهبود بخشد، مانند استفاده از مینی‌دسته‌ها (mini-batches) در جای‌جای محاسبه گرادیان و استفاده از روش‌های بهبود گرادیان مانند Momentum، RMSprop و Adam. به طور کلی، گرادیان کاهشی یک الگوریتم قدرتمند و مهم در یادگیری ماشین و بهینه‌سازی است و در بسیاری از مسایل واقعی استفاده می‌شود.

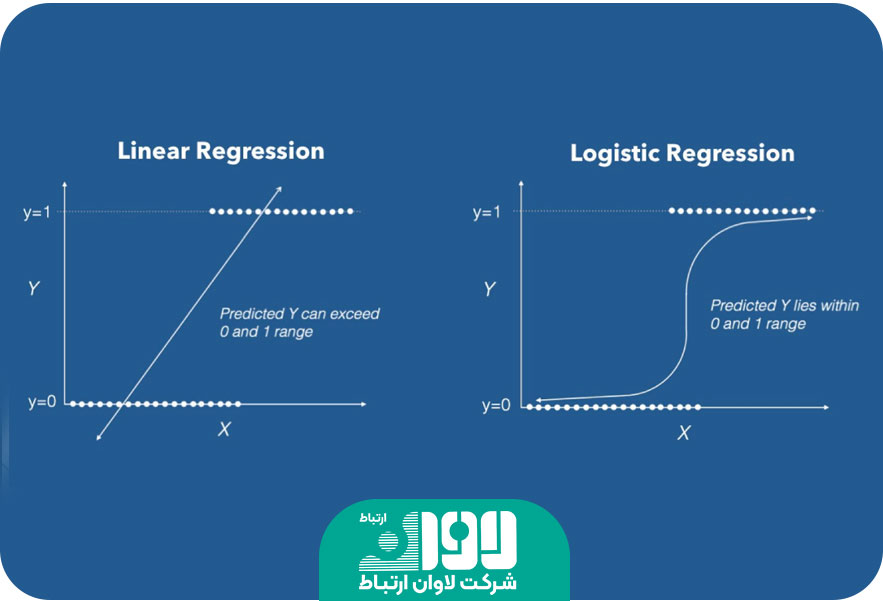
مقایسه رگرسیون خطی و رگرسیون لجستیک

همان‌گونه که اشاره کردیم رگرسیون لجستیک (Logistic Regression) یک الگوریتم یادگیری ماشین است که برای مسایل دسته‌بندی دوگانه استفاده می‌شود. عملکرد رگرسیون لجستیک به این صورت است که ابتدا باید مقادیر اولیه برای پارامترها تعیین شوند. این پارامترها معمولا به صورت تصادفی انتخاب می‌شوند. با استفاده از مقادیر فعلی پارامترها و ویژگی‌های ورودی، خروجی لجستیک برای هر نمونه ورودی محاسبه می‌شود. خروجی لجستیک بین 0 و 1 قرار دارد و نشان می‌دهد که هر نمونه به کدام کلاس تعلق دارد. برای اندازه‌گیری خطا یا هزینه از تابع هزینه لجستیک (Logistic Loss) استفاده می‌شود. این تابع هزینه معمولا مبتنی بر تابع لگاریتمی است و مقدار خطا را برای پارامترهای فعلی مدل محاسبه می‌کند. برای به‌روزرسانی پارامترها به جهت کمینه کردن تابع هزینه، نیاز به محاسبه گرادیان تابع هزینه نسبت به پارامترها داریم. این گرادیان معمولا با استفاده از قاعده زنجیره‌ای (chain rule) و مشتق‌گیری جزئی تابع هزینه نسبت به هر پارامتر محاسبه می‌شود. با استفاده از گرادیان محاسبه شده، پارامترها را به صورت معکوس گرادیان به‌روزرسانی می‌کنیم. این عملیات به صورت مکرر تکرار می‌شود تا به یک شرایط همگرایی برسیم. مشابه گرادیان کاهشی، بررسی می‌کنیم که آیا به شرایط توقف موردنظر رسیده‌ایم یا خیر. این شرایط می‌توانند شامل تعداد مشخصی تکرار، دست‌یابی به مقدار معینی برای تابع هزینه یا تغییر کمتر از یک آستانه مشخص در پارامترها باشند. اگر الگوریتم هنوز به شرایط توقف نرسیده است به مرحله پس از تعیین مقادیر اولیه می‌رویم، پارامترها را به‌روزرسانی کرده و فرآیند محاسبه تابع هزینه را انجام می‌دهیم تا سرانجام به نتیجه دلخواه برسیم. این مراحل به صورت تکراری انجام می‌شوند تا مقادیر پارامترها به یک مقدار بهینه همگرا شوند و تابع هزینه کمینه شود.

متغیر و نوع خروجی

در رگرسیون لجستیک، ورودی‌ها شامل مجموعه‌ای از ویژگی‌ها یا متغیرها هستند که برای پیش‌بینی یک متغیر وابسته دوگانه (دسته‌بندی دوگانه) استفاده می‌شوند. این متغیر وابسته می‌تواند دو حالت 0 و 1 را به خود بگیرد. متغیرهای ورودی می‌توانند به صورت متغیرهای دسته‌ای (categorical variables) و متغیرهای عددی (numerical variables) باشند. متغیرهای دسته‌ای معمولا به صورت متغیرهای دودویی (binary variables) یا متغیرهای چنددسته‌ای (multiclass variables) تعریف می‌شوند. متغیرهای عددی نیز می‌توانند مقادیر پیوسته (continuous values) یا مقادیر گسسته (discrete values) را داشته باشند. خروجی رگرسیون لجستیک یک احتمال است که بین 0 و 1 قرار دارد و نشان می‌دهد که هر نمونه ورودی به کدام کلاس (مقدار 0 یا 1) تعلق دارد. اگر احتمال خروجی بیشتر از 0.5 باشد، نمونه ورودی به کلاس 1 تعلق دارد و اگر احتمال کمتر از 0.5 باشد، به کلاس 0 تعلق دارد.

ارتباط میان متغیرها

در رگرسیون لجستیک، ارتباط میان متغیرها برای پیش‌بینی متغیر وابسته (خروجی) استفاده می‌شود. برای بررسی ارتباط میان متغیرها، می‌توان از معیارهایی مانند ضریب همبستگی (correlation coefficient)، ماتریس همبستگی (correlation matrix) و آزمون فرضیه استفاده کرد. ضریب همبستگی نشان می‌دهد که دو متغیر به چه اندازه با یکدیگر همبستگی دارند. مقدار ضریب همبستگی بین -1 و 1 قرار می‌گیرد. مقدار صفر نشان‌دهنده عدم وجود همبستگی است، مقدار 1 نشان‌دهنده همبستگی مثبت کامل و مقدار -1 نشان‌دهنده همبستگی منفی کامل است.

ماتریس همبستگی شامل ضرایب همبستگی بین همه جفت متغیرها است. با استفاده از ماتریس همبستگی می‌توانید الگوهای همبستگی بین متغیرها را بررسی کنید و متغیرهایی که همبستگی قوی دارند را تشخیص دهید.

برای بررسی میزان اهمیت و ارتباط معنادار بین متغیرها و خروجی، می‌توان آزمون فرضیه مورد استفاده قرار داد. این آزمون‌ها می‌توانند شامل آزمون t، آزمون F یا آزمون chi-square test باشند، که بسته به نوع متغیرها و توزیع آن‌ها انتخاب می‌شوند. با تحلیل ارتباط میان متغیرها، می‌توانید متغیرهای مهم و تاثیرگذار بر پیش‌بینی متغیر وابسته را شناسایی کنید و در مدل رگرسیون لجستیک استفاده کنید.

همبستگی میان متغیرهای مستقل

برای بررسی همبستگی میان متغیرهای مستقل در رگرسیون لجستیک، می‌توان از ضریب همبستگی نقطه‌ای (point-biserial correlation) و آزمون فرضیه استفاده کرد. ضریب همبستگی نقطه‌ای برای بررسی همبستگی بین یک متغیر دودویی و یک متغیر عددی استفاده می‌شود و بین -1 و 1 قرار دارد. مقدار صفر نشان‌دهنده عدم وجود همبستگی است، مقدار 1 نشان‌دهنده همبستگی مثبت کامل و مقدار -1 نشان دهنده همبستگی منفی کامل است. برای بررسی معنادار بودن همبستگی میان متغیرهای مستقل، می‌توان از آزمون فرضیه استفاده کرد. در رگرسیون لجستیک، می‌توان از آزمون t استفاده کرد تا بررسی شود که آیا میانگین متغیرهای عددی در دو گروه متفاوت (بر اساس متغیر دودویی) معنادارا متفاوت هستند یا خیر. به طور کلی، همبستگی میان متغیرهای مستقل می‌تواند نشان‌دهنده وجود رابطه و تاثیر متقابل بین این متغیرها باشد. این اطلاعات می‌توانند در انتخاب متغیرهای مهم و تاثیرگذار بر پیش‌بینی متغیر وابسته در مدل رگرسیون لجستیک مفید باشند.

وزن و مشاهدات

در رگرسیون لجستیک، وزن‌دهی به مشاهدات می‌تواند در تعیین تاثیر مشاهدات بر مدل و پیش‌بینی متغیر وابسته مفید باشد. وزن‌دهی به مشاهدات به معنی اختصاص وزن مختلف به هر مشاهده است که نشان‌دهنده اهمیت آن مشاهده در مدل است. وزن‌دهی به مشاهدات می‌تواند در مواردی مفید باشد که مشاهدات دارای وزن‌های مختلفی هستند و می‌خواهید تاثیر برخی مشاهدات بیشتر از دیگران باشد. برای مثال، اگر در مجموعه داده خود دارای نمونه‌هایی با تعداد کمی مشاهدات هستید و نمونه‌های دیگر با تعداد بیشتر، ممکن است بخواهید نمونه‌های با تعداد بیشتر مشاهدات را بیشتر مورد توجه قرار دهید تا تاثیر آن‌ها در مدل بیشتر شود. وزن‌دهی به مشاهدات می‌تواند به صورت مستقیم با استفاده از وزن‌های مشخص برای هر مشاهده انجام شود. این وزن‌ها می‌توانند به صورت دستی تعیین شوند یا با استفاده از روش‌های مشخصی مانند وزن‌دهی معکوس فراوانی (inverse frequency weighting) محاسبه شوند.

همچنین، در بعضی از نرم‌افزارها و کتابخانه‌های آماری، امکان استفاده از وزن‌دهی به مشاهدات در مدل رگرسیون لجستیک وجود دارد و می‌توانید وزن‌ها را به عنوان یک ورودی در نظر بگیرید تا تاثیر مشاهدات مختلف را مدل کنید.

توابع فعال‌سازی

توابع فعال‌سازی (activation functions) عمدتا در شبکه‌های عصبی استفاده می‌شوند تا خروجی یک نورون را تنظیم کرد. این توابع عملکرد غیرخطی دارند و نقش مهمی در ایجاد پیچیدگی و قابلیت تعمیم شبکه‌های عصبی دارند. برخی از رایج در دنیای یادگیری ماشین و شبکه‌های عصبی به شرح زیر است.

تابع سیگمویید (Sigmoid): فرمول تابع سیگمویید به صورت زیر است:

   f(x) = 1 / (1 + exp(-x))

این تابع مقدار ورودی را به مقداری بین 0 و 1 تبدیل می‌کند و برای مسایل دودویی یا احتمالاتی مناسب است. با افزایش ورودی به مثبت یا منفی بی‌نهایت میل می‌کند و مشکل محوشدگی گرادیان را به وجود می‌آورد.

تابع ReLU (Rectified Linear Unit): فرمول تابع ReLU به صورت زیر است:

   f(x) = max(0, x)

این تابع ورودی را به مدل خطی تبدیل می‌کند و برای مسایلی که تحلیل غیرخطی نیاز ندارند، به خصوص در شبکه‌های عمیق، بسیار موثر است. با این حال، مشکلی به نام “مرگ نورون” وجود دارد به این معنا که اگر خروجی نورون در مرحله‌ای همواره صفر باشد، به دلیل مشتق صفر در نقطه صفر، نورون دیگری بر روی آن تاثیری نخواهد گذاشت.

تابع تانژانت هیپربولیک (Hyperbolic Tangent): فرمول تابع تانژانت هیپربولیک به صورت زیر است:

   f(x) = (exp(x) – exp(-x)) / (exp(x) + exp(-x))

این تابع، مقدار ورودی را به مقداری بین -1 و 1 تبدیل می‌کند. مشابه تابع سیگموئید است اما با دامنه خروجی گسترده‌تر. از آن برای مسایلی که نیاز به مقادیر منفی و مثبت دارند، استفاده می‌شود.

تابع softmax: تابع softmax معمولا در لایه آخر شبکه‌های عصبی برای دسته‌بندی چندکلاسه استفاده می‌شوند. این تابع مقادیر ورودی را به صورت یک توزیع احتمالی بین 0 و 1 تبدیل می‌کند که مجموع مقادیر آن برابر با 1 است. فرمول تابع softmax به صورت زیر است:

   f(x_i) = exp(x_i) / (sum(exp(x_j)) for j in range(n))

در این فرمول، x_i مقدار ورودی نورون i و n تعداد نورون‌ها است.

لازم به توضیح است که توابع فعال‌سازی دیگری نیز وجود دارند که بسته به نوع مساله و ساختار شبکه می‌توانند استفاده شوند، از جمله تابع خطی (Linear), تابع Swish, تابع Leaky ReLU و غیره. انتخاب تابع فعال‌سازی مناسب بسته به خصوصیات مساله و نوع شبکه بستگی دارد.

بخوانید: یک دانشمند داده به چه مباحث کاربردی ریاضیات پایه نیاز دارد؟