زمان خواندن: 18 دقیقه 

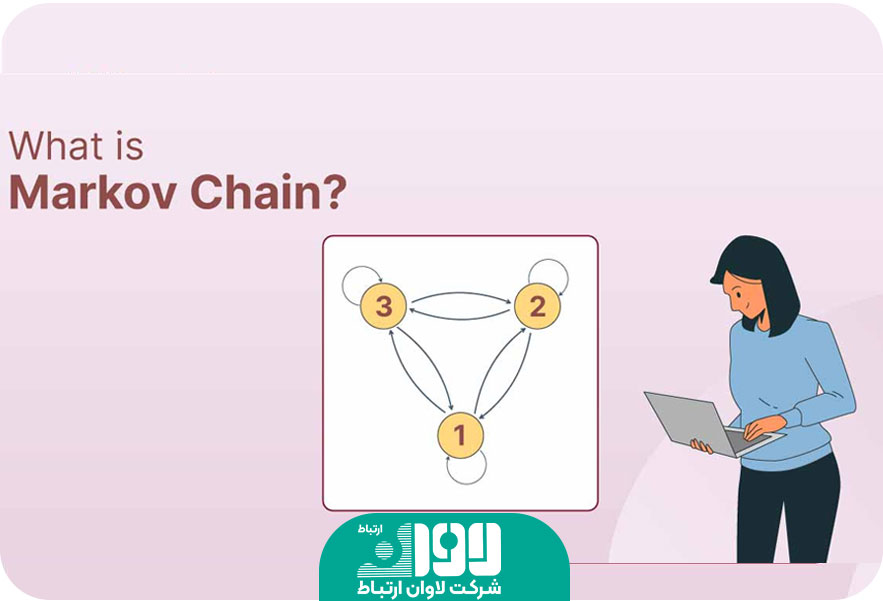
زنجیره مارکوف یک مدل احتمالاتی است که برای مدل‌سازی فرایندهای تصادفی به کار می‌رود. این مدل بر اساس فرضیه‌ مارکوف که احتمال وقوع یک رویداد در آینده را به وقوع پیشینه‌ آن مرتبط می‌داند، طراحی شده است. در زنجیره مارکوف، فرایند تصادفی را می‌توان به صورت مجموعه‌ای از حالت‌ها و گذرهای بین این حالت‌ها مدل کرد. هر حالت با یک رویداد یا شرایط مشخص در سیستم مرتبط است و گذارها نشان‌دهنده‌ تغییر وضعیت از یک حالت به حالت دیگر هستند. همچنین، هر حالت با احتمالی مشخص به حالت‌های دیگر منتقل می‌شود.

یک زنجیره مارکوف می‌تواند دارای دو خاصیت مهم باشد: خاصیت مارکوف و خاصیت پایداری. خاصیت مارکوف به این معنی است که احتمال وقوع یک حالت در زمان t+1، تنها به حالت فعلی در زمان t وابسته است و وابستگی به تاریخچه‌ قبلی ندارد. خاصیت پایداری به این معنی است که هر وضعیت قابل رسیدن به هر حالت دیگری است. از زنجیره‌های مارکوف در مدل‌سازی و پیش‌بینی رویدادها در حوزه‌های مختلفی مانند علوم رایانه، آمار، اقتصاد، مهندسی، بیولوژی و غیره استفاده می‌شود. این مدل می‌تواند در تحلیل داده‌های زمانی، تشخیص الگوها، پیش‌بینی و تصمیم‌گیری مورد استفاده قرار بگیرد.

تئوری فرآیندهای تصادفی چیست

تئوری فرآیندهای تصادفی مجموعه‌ای از اصول و تکنیک‌های ریاضی است که برای مدل‌سازی و تحلیل رفتار فرایندهای تصادفی استفاده می‌شود. فرآیندهای تصادفی مجموعه‌ای از متغیرهای تصادفی هستند که توسط یک مجموعه قوانین احتمالاتی تعریف می‌شوند و در طول زمان تغییر می‌کنند. تئوری فرآیندهای تصادفی مفاهیم و ابزارهایی را ارائه می‌دهد که به ما امکان می‌دهد ویژگی‌های مختلف فرآیندهای تصادفی را مدل کنیم و خصوصیات آن‌ها را بررسی کنیم. این تئوری شامل مفاهیم اساسی مانند فضای نمونه‌ای، متغیر تصادفی، تابع توزیع احتمال، تابع چگالی احتمال، تابع توزیع تجمیعی و مفاهیم پیشرفته‌تری مانند استمراری بودن، استمراری بودن زمان، استمراری بودن مسیر، وابستگی زمانی، استقلال و استراحت زمانی است.

با استفاده از تئوری فرآیندهای تصادفی، می‌توانیم فرآیندهای تصادفی را با مدل‌های ریاضی توصیف کنیم و خصوصیات آن‌ها را بررسی کنیم. همچنین، این تئوری ابزارها و تکنیک‌هایی را فراهم می‌کند که می‌توان از آن‌ها برای پیش‌بینی، تحلیل و بهینه‌سازی در مسایل مختلفی مانند مهندسی، علوم رایانه، آمار و اقتصاد استفاده کرد. تئوری فرآیندهای تصادفی به عنوان یکی از مبانی اصلی در آمار و احتمالات و بسیاری از حوزه‌های علمی و فنی مورد استفاده قرار می‌گیرد و به ما امکان می‌دهد تا رفتار و الگوهای تصادفی در داده‌ها را توصیف و تحلیل کنیم.

چه نوع مسایلی می‌توان با استفاده از تئوری فرآیندهای تصادفی حل کرد؟

تئوری فرآیندهای تصادفی قابلیت حل و مدل‌سازی مسائل متنوعی را در بسیاری از حوزه‌های علمی و فنی فراهم می‌کند. به طور مثال، در مهندسی، تئوری فرآیندهای تصادفی در مدل‌سازی و تحلیل سیستم‌های پیچیده با رفتار تصادفی مانند شبکه‌های ترافیکی، سیستم‌های مخابراتی، سیستم‌های تولید و موارد دیگر استفاده می‌شود. مثال‌هایی از مسایل مهندسی که با استفاده از تئوری فرآیندهای تصادفی قابل حل هستند شامل طراحی و بهینه‌سازی شبکه‌های ارتباطی، برنامه‌ریزی تولید، مدل‌سازی پهنای باند شبکه‌ها و غیره می‌شود. در علوم  رایانه، تئوری فرآیندهای تصادفی در مدل‌سازی و تحلیل الگوریتم‌های تصادفی، شبکه‌های عصبی، پردازش سیگنال‌ها و تصاویر، الگوریتم‌های بهینه‌سازی و سیستم‌های توزیع شده مورد استفاده قرار می‌گیرد.

این مفهوم قدرتمند بستر اصلی تحلیل و پیش‌بینی داده‌های زمانی است. از طریق مدل‌سازی فرآیندهای تصادفی می‌توان الگوهای زمانی، رشد و کاهش، روند‌ها و تغییرات تصادفی در داده‌ها را تحلیل کرد. همچنین، با استفاده از تئوری فرآیندهای تصادفی می‌توان مسایلی مانند پیش‌بینی سری‌های زمانی، تحلیل ریسک مالی، آزمون فرضیه‌ها و مدل‌سازی سیستم‌های پیچیده را حل کرد. در حوزه اقتصاد و مالی، تئوری فرآیندهای تصادفی استفاده‌های فراوانی دارد. می‌توان از آن‌ها برای مدل‌سازی و پیش‌بینی قیمت‌های سهام و ارزها، تحلیل ریسک و مدیریت پرتفوی (سبد سهام)، تحلیل و پیش‌بینی رشد اقتصادی و سایر مسایل مرتبط با بازارهای مالی استفاده کرد. بد نیست بدانید که ما از تئوری فرآیندهای تصادفی در مدل‌سازی و تحلیل فرآیندهای طبیعی مانند رشد جمعیت، الگوهای هواشناسی، تغییرات اقلیمی، توزیع آب و غیره نیز استفاده می‌کنیم.

این تکنیک‌ها می‌توانند به ما در درک بهتر مکانیسم‌های پشت صحنه این فرآیندها کمک کنند و در برنامه‌ریزی منابع و مدیریت محیط زیست مفید باشند. در حوزه پزشکی نیز به منظور مطالعه بیماری‌های مزمن، مدل‌سازی و پیش‌بینی پاسخ‌های دارویی، تحلیل سیگنال‌های پزشکی و طبیعی، طراحی آزمایش‌ها و مدل‌سازی اپیدمیولوژیک کاربرد دارند. در نهایت در علوم اجتماعی، تئوری فرآیندهای تصادفی می‌تواند در مدل‌سازی و تحلیل رفتار اجتماعی، پخش شایعه‌ها و انتشار اطلاعات، مدل‌سازی شبکه‌های اجتماعی و سیستم‌های تعاملی انسانی مورد استفاده قرار گیرد. موارد یاد شده تنها چند مثال از حوزه‌هایی هستند که تئوری فرآیندهای تصادفی در آن‌ها به کار می‌رود. با توجه به گستردگی و کاربرد‌های این تئوری، می‌توان گفت مسایلی که می‌توان با استفاده از تئوری فرآیندهای تصادفی حل کرد، بسیار گسترده و متنوع هستند.

زنجیره مارکوف و فرآیند مارکوف زمان-گسسته

زنجیره مارکوف و فرآیند مارکوف زمان-گسسته دو مفهوم مرتبط در تئوری فرآیندهای تصادفی هستند.

1. زنجیره مارکوف: زنجیره مارکوف به یک دنباله از وضعیت‌ها یا حالت‌ها که در طول زمان تغییر می‌کنند و وابسته به وضعیت‌های قبلی هستند، اشاره دارد. این وابستگی به صورت ویژگی مارکوف به معنای عدم استفاده از حافظه است. به بیان دقیق‌تر وضعیت فعلی تنها به وضعیت قبلی وابسته است و تاریخچه بیشتر شامل نمی‌شود. زنجیره مارکوف می‌تواند در موارد متنوعی مورد استفاده قرار گیرد، از جمله پیش‌بینی وضعیت‌های آینده بر اساس وضعیت‌های کنونی، مدل‌سازی و پیش‌بینی رشد جمعیت، تحلیل رفتار سیستم‌های پیچیده مانند شبکه‌های اجتماعی و سیستم‌های طبیعی، مدل‌سازی فرآیندهای تصمیم‌گیری و غیره.
2. فرآیند مارکوف زمان-گسسته: فرآیند مارکوف زمان-گسسته نوعی فرآیند تصادفی است که وضعیت‌ها در زمان‌های گسسته و به طور یکنواخت تغییر می‌کنند. در این فرآیند، وضعیت فعلی تنها به وضعیت قبلی وابسته است و فرآیند از خاصیت عدم حافظه برخوردار است. فرآیند مارکوف زمان-گسسته به طور گسترده در مدل‌سازی و تحلیل سیستم‌های پیچیده استفاده می‌شود. مثال‌هایی از این کاربردهای این مهفوم را باید در مدل‌سازی رفتار مشتریان در صنعت خدمات، تحلیل صف‌ها و صف‌های انتظار، مدل‌سازی روند تصمیم‌گیری، پیش‌بینی رشد بیماری‌ها در اپیدمیولوژی، مدل‌سازی سیستم‌های توزیع شده و غیره است.

به طور خلاصه، زنجیره مارکوف و فرآیند مارکوف زمان-گسسته ابزارهای مهم در تئوری فرآیندهای تصادفی هستند که در مدل‌سازی و تحلیل مسائل مختلف از جمله مسائل مهندسی، علوم رایانه، آمار و احتمالات، علوم اجتماعی وسایر حوزه‌های علمی به کار می‌روند. این دو مفهوم با یکدیگر مرتبط هستند و استفاده از زنجیره مارکوف می‌تواند به مدل‌سازی و پیش‌بینی رفتار فرآیند مارکوف زمان-گسسته کمک کند.

خصوصیات زنجیره مارکوف

زنجیره مارکوف دارای یکسری خصوصیت مهم است که عملکردش را بهتر شرح می‌دهند. اولین مورد عدم حافظه است. یکی از ویژگی‌های مهم زنجیره مارکوف، خاصیت عدم حافظه است. همان‌گونه که اشاره کردیم، ویژگی فوق به این معنا است که وضعیت فعلی زنجیره تنها به وضعیت قبلی آن وابسته است و تاریخچه بیشتری را در نظر نمی‌گیرد. به عبارت دیگر، با داشتن وضعیت فعلی، اطلاعاتی درباره وضعیت‌های گذشته به دست نمی‌آوریم. این خاصیت عدم حافظه باعث ساده‌تر شدن مدل‌سازی و تحلیل زنجیره می‌شود. مورد بعد احتمال انتقال است. زنجیره مارکوف با استفاده از ماتریس احتمالات انتقال (Transition Probability Matrix) توصیف می‌شود. این ماتریس، احتمال انتقال از یک وضعیت به وضعیت دیگر را بیان می‌کند. در یک زنجیره مارکوف با n وضعیت ممکن، ماتریس احتمالات انتقال اندازه‌ای به ابعاد n × n دارند. عناصر این ماتریس نشان می‌دهند که با چه احتمالی از هر وضعیت به هر وضعیت دیگری منتقل می‌شویم.

ویژگی بعدی استمرار زمانی است. زنجیره مارکوف معمولا به صورت زمان-گسسته مدل‌سازی می‌شود، یعنی وقت را به بازه‌های گسسته تقسیم می‌کند. بنابراین، زمان به صورت متناوب در مراحل گسسته جلو می‌رود و وضعیت زنجیره در هر مرحله مشخص می‌شود. این گسستگی در زمان، تحلیل و مدل‌سازی را ساده‌تر می‌کند، زیرا می‌توانیم رویدادهای مختلف را در گام‌های متمایز مدل‌سازی کنیم.

خصوصیت جالب بعدی قابلیت دسته‌بندی است. زنجیره مارکوف را می‌توان بر اساس وضعیت‌های آن به دسته‌های مختلف تقسیم کرد. این دسته‌بندی می‌تواند بر اساس خواص ویژه‌ای که در هر وضعیت وجود دارد، انجام شود. این دسته‌بندی می‌تواند در تحلیل و پیش‌بینی رفتار مفید باشد و نقش مهمی در فهم سیستم داشته باشد. یک زنجیره مارکوف ممکن است به یک حالت توازن برسد که در آن توزیع احتمال وضعیت‌ها ثابت می‌شود و تغییر نمی‌کند. این توازن می‌تواند با ماتریس توازن نشان داده شود که در آن بردار توازن نسبت به ماتریس احتمالات انتقال، برداری است که مضرب سمت راست آن با ماتریس احتمالات انتقال برابر با خود بردار توازن می‌شود. در حالت توازن، توزیع احتمال وضعیت‌ها در طول زمان ثابت می‌ماند.

یکی از کاربردهای مهم زنجیره مارکوف، قابلیت پیش‌بینی آینده بر اساس وضعیت کنونی است. با داشتن وضعیت فعلی، می‌توان با استفاده از ماتریس احتمالات انتقال، احتمال وقوع وضعیت‌های آینده را محاسبه کرد. این قابلیت پیش‌بینی می‌تواند در بسیاری از حوزه‌ها، از جمله علوم رایانه، مهندسی، آمار و احتمالات، اقتصاد و غیره مورد استفاده قرار گیرد. در زنجیره مارکوف، مسیرهایی که از یک وضعیت به وضعیت دیگر می‌روند، می‌توانند بررسی شوند. مطالعه و تحلیل مسیرهای مارکوف می‌تواند به درک بهتر رفتار زنجیره و مدلسازی آن کمک کند.

زنجیره مارکوف مرتبه k– با حافظه

زنجیره مارکوف مرتبه k- با حافظه (kth-order Markov chain) یک توسعه از زنجیره مارکوف است که اطلاعاتی از k وضعیت گذشته را در نظر می‌گیرد. در زنجیره مارکوف معمولی، فقط به وضعیت قبلی وابسته هستیم، اما در زنجیره مارکوف مرتبه k-، وضعیت فعلی به k وضعیت گذشته وابسته است. برای مدل‌سازی زنجیره مارکوف مرتبه k-، احتمال انتقال بین وضعیت‌ها باید به شکل یک ماتریس k-بعدی مدل‌سازی شود. به عبارت دیگر، برای هر ترکیب از k وضعیت، احتمال انتقال به وضعیت بعدی مشخص می‌شود.

مزیت استفاده از زنجیره مارکوف مرتبه k- با حافظه، افزودن اطلاعات بیشتر در مدل‌سازی است. با در نظر گرفتن k وضعیت گذشته، توالی‌های طولانی‌تر و الگوهای پیچیده‌تری را می‌توان درک کرد. این مدل‌سازی مناسب است برای مواردی که وابستگی‌های زمانی بلندمدت و مهم هستند و اطلاعات گذشته تاثیر قابل توجهی بر رویدادهای آینده دارند. به عنوان مثال، در زبان‌شناسی، زنجیره مارکوف مرتبه k- با حافظه می‌تواند استفاده شود تا ترتیب واژگان در یک جمله را مدل کند. با در نظر گرفتن k واژه گذشته، احتمال وقوع واژه بعدی قابل پیش‌بینی است. این مدل‌سازی می‌تواند در بررسی ساختار زبانی و تولید جملات مفید باشد. به طور کلی، زنجیره مارکوف مرتبه k- با حافظه قابلیت مدلسازی رفتارهای پیچیده‌تر را ارائه می‌دهد و می‌تواند در حوزه‌های مختلفی مانند پردازش زبان طبیعی، تحلیل سیستم‌ها، پیش‌بینی مالی و غیره مورد استفاده قرار گیرد.

زنجیره مارکوف تناوبی (Periodic)

زنجیره مارکوف تناوبی (Periodic Markov chain) یک نوع خاص از زنجیره مارکوف است که در آن وضعیت‌ها به صورت تناوبی تکرار می‌شوند. به عبارت دیگر، ممکن است زنجیره به طور متناوب بین یک مجموعه محدودی از وضعیت‌ها حرکت کند. در یک زنجیره مارکوف تناوبی، هر وضعیت به دو دسته تقسیم می‌شود: وضعیت‌های تناوبی و وضعیت‌های غیرتناوبی. وضعیت‌های تناوبی در مدت زمانی معین به صورت تناوبی تکرار می‌شوند، در حالی که وضعیت‌های غیرتناوبی تناوب ندارند و به صورت غیرمنظم در زنجیره ظاهر می‌شوند.

در زنجیره مارکوف تناوبی، ماتریس انتقال (transition matrix) نیز یک الگوی تناوبی دارد. به عبارت دقیق‌تر، اگر وضعیت i یک وضعیت تناوبی باشد، باید احتمال انتقال به وضعیت تناوبی دیگری (مانند j) در مرحله بعدی برابر باشد. به عبارت ساده‌تر، احتمال انتقال بین وضعیت‌های تناوبی در هر مرحله یکسان است. زنجیره مارکوف تناوبی به دلیل وجود تناوب در وضعیت‌ها، رفتار پیچیده‌تری نسبت به زنجیره‌های مارکوف معمولی دارد. ممکن است زمانی که به یک وضعیت تناوبی رسیده‌ایم، به صورت متناوب در آن حبس شویم و به وضعیت‌های غیرتناوبی دسترسی نداشته باشیم.

زنجیره مارکوف تناوبی در مدلسازی برخی از سیستم‌ها و فرآیندهای زمانی که رفتار دوره‌ای دارند، مفید است. به عنوان مثال، در مسائل مربوط به ترافیک شهری، الگوهای تناوبی در ترافیک صبح و عصر روز وجود دارد. همچنین، در مسایل مربوط به مدلسازی رفتار اقتصادی و مالی نیز می‌توان از زنجیره مارکوف تناوبی استفاده کرد. برای مدلسازی زنجیره مارکوف تناوبی، می‌توان از مفاهیم و روش‌های زنجیره مارکوف معمولی استفاده کرد با این تفاوت که باید به تناوب در وضعیت‌ها دقت کرد و ماتریس انتقال را به طور متناوب تنظیم کرد. همچنین، برای تحلیل زنجیره مارکوف تناوبی، مفاهیمی مانند ماتریس احتمال تجمعی و توزیع پایدار نیز مورد استفاده قرار می‌گیرند. در کل، زنجیره مارکوف تناوبی برای مدلسازی سیستم‌هایی با الگوهای تناوبی و دوره‌ای مفید است. این مدلسازی می‌تواند در برخی از حوزه‌ها مانند تحلیل زمان سری، پیش‌بینی زمانی، بهینه‌سازی برنامه‌ریزی و سیستم‌های پویا مورد استفاده قرار گیرد.

مدل پنهان مارکوف (Hidden Markov Model)

مدل پنهان مارکوف (Hidden Markov Model یا HMM) یک مدل احتمالاتی است که در آن سری زمانی از وضعیت‌ها و سری زمانی از مشاهدات وجود دارد. در این مدل، وضعیت‌ها به صورت پنهان هستند و نمی‌توان آن‌ها را به طور مستقیم مشاهده کرد. اما مشاهدات به شکلی غیرمستقیم وابسته به وضعیت‌ها در دسترس است. مدل پنهان مارکوف از سه مجموعه اساسی تشکیل شده است:

1. مجموعه وضعیت‌ها (States): این مجموعه شامل وضعیت‌های پنهان است که در هر لحظه مشخص می‌کنند که سیستم در چه حالتی قرار دارد. به طور مثال، در مدلسازی زبان طبیعی، وضعیت‌ها می‌توانند بیانگر حالت‌های مختلف گفتار (مانند حرف یا صدا) باشند.
2. مجموعه مشاهدات (Observations): این مجموعه شامل مشاهدات غیرمستقیم است که به صورت مشاهداتی مشاهده می‌شوند و با وضعیت‌ها در ارتباط هستند. به طور مثال در مدلسازی زبان طبیعی، مشاهدات می‌توانند بیانگر کلمات یا واژگان مشاهده شده توسط یک گوینده باشند.
3. ماتریس انتقال (Transition Matrix): این ماتریس نشان می‌دهد که با احتمال چه مقداری، سیستم از یک وضعیت به وضعیت دیگر منتقل می‌شود. به عبارت دیگر، احتمال انتقال بین وضعیت‌ها در زمان تغییر می‌کند. ماتریس انتقال می‌تواند نشان دهنده مدل تغییرات زمانی در سیستم باشد.

مدل پنهان مارکوف مبتنی بر فرضیه انتخاب بیشینه (Maximum Likelihood) است و با استفاده از الگوریتم‌هایی مانند الگوریتم Viterbi و الگوریتم Baum-Welch می‌توان از طریق آموزش مدل، پارامترهای ماتریس انتقال و توزیع احتمال مشاهدات را تخمین زد. مدل پنهان مارکوف در حوزه‌های مختلفی از جمله پردازش زبان طبیعی، تشخیص گفتار، ترجمه ماشینی، تحلیل سیگنال‌ها، بینایی ماشین و بسیاری از مسائل سری زمانی مورد استفاده قرار می‌گیرد.

الگوریتم Viterbi در خدمت مدل پنهان مارکوف

الگوریتم Viterbi یک الگوریتم پویای برنامه‌ریزی است که در مدل پنهان مارکوف (HMM) استفاده می‌شود. این الگوریتم برای یافتن مجموعه بهینه‌ای از وضعیت‌های پنهان در یک HMM بر اساس مشاهدات غیرمستقیم استفاده می‌شود. به طور خاص، الگوریتم Viterbi برای یافتن مسیری از وضعیت‌های پنهان با بیشترین احتمال استفاده می‌شود که باعث تولید مشاهدات مشاهده شده می‌شود. عملکرد الگوریتم Viterbi به شرح زیر است:

1. مقداردهی اولیه:

   – مقدار اولیه برای وضعیت اول (به طور مثال وضعیت شروع) را تعیین کنید.

   – برای هر وضعیت، مقدار اولیه برابر با ضرب احتمال اولیه وضعیت در احتمال مشاهدات در وضعیت را قرار دهید.

2. برای هر مشاهده غیرمستقیم در ترتیب زمانی:

   – برای هر وضعیت ممکن:

     – محاسبه احتمال بیشترین مسیر که به وضعیت فعلی می‌رسد.

     – ضرب این احتمال در احتمال انتقال از وضعیت قبلی به وضعیت فعلی.

     – انتخاب بزرگترین مقدار برای مسیر قبلی و ضرب آن در احتمال انتقال بیشترین مسیر به وضعیت فعلی.

     – ذخیره کردن احتمال بیشترین مسیر در وضعیت فعلی و نشان دادن مسیر بیشترین احتمال.

3. پایان الگوریتم:

   – برای مشاهده آخرین، احتمال بیشترین مسیر را محاسبه کنید.

   – از انتهای مسیر بیشترین احتمال به عقب بروید و مسیر بهینه را بازسازی کنید.

با اجرای الگوریتم Viterbi بر روی یک مدل پنهان مارکوف، می‌توانید مجموعه بهینه‌ای از وضعیت‌های پنهان را که باعث تولید مشاهدات مشاهده شده می‌شود، به دست آورید. این الگوریتم برای بسیاری از کاربردهای HMM مانند تشخیص گفتار، ترجمه ماشینی و تحلیل سیگنال‌ها بسیار مفید است.

مدل پنهان مارکوف در چه حوزه‌هایی به کار می‌رود؟

مدل پنهان مارکوف (HMM) در حوزه‌های مختلفی از جمله زبان طبیعی، گفتار، بینایی ماشین، ترجمه ماشینی، تشخیص الگو، تحلیل سیگنال‌ها و موارد دیگر استفاده می‌شود. برخی از این حوزه‌ها به شرح زیر هستند.

1. پردازش زبان طبیعی: HMM در پردازش زبان طبیعی استفاده می‌شود، برای مثال در تشخیص قسمت‌های مختلف گفتاری مانند کلمات و فاصله‌گذاری بین آن‌ها، تشخیص قسمت‌های مختلف جملات مانند اسم، فعل و حرف اضافه و همچنین در ترجمه ماشینی.
2. تشخیص گفتار: با استفاده از HMM می‌توان مدل‌های شناسایی گفتار را آموزش داد و در تشخیص و تحلیل گفتار استفاده کرد. این مدل‌ها می‌توانند برای تشخیص کلمات، شناسایی ساختار جمله، تشخیص مکالمات و بسیاری دیگر از کاربردهای گفتاری مفید باشند.
3. بینایی ماشین: در بینایی ماشین، HMM می‌تواند برای تشخیص الگو، تشخیص شی، تشخیص حرکت و ردیابی اشیا استفاده شود. با استفاده از HMM می‌توان الگوهایی را در تصاویر شناسایی کرد و اشیا را در تصاویر تشخیص داد.
4. ترجمه ماشینی: HMM می‌تواند در ترجمه ماشینی بین دو زبان مختلف استفاده شود. با استفاده از HMM می‌توان مدلی را آموزش داد که بتواند جملات یک زبان را به جملات دیگر ترجمه کند.
5. تحلیل سیگنال‌ها: HMM در تحلیل سیگنال‌ها مانند سیگنال‌های صوتی، سیگنال‌های مخابراتی و سیگنال‌های الکترونیکی استفاده می‌شود. با استفاده از HMM می‌توان الگوهای مختلف سیگنال‌ها را تشخیص داد و آن‌ها را تحلیل کرد.

موارد یاد شده تنها چند نمونه از حوزه‌هایی هستند که HMM در آن‌ها قابل استفاده است. به عنوان یک مدل احتمالاتی و قابل تعمیم، HMM می‌تواند در بسیاری از مسایل سری زمانی و مسایلی که داده‌های پنهان و وابسته به آن‌ها وجود دارد، قابل استفاده است.

تفاوت بین مدل پنهان مارکوف و شبکه عصبی بازگشتی در حوزه پردازش زبان طبیعی

در حوزه پردازش زبان طبیعی (Natural Language Processing)، مدل پنهان مارکوف (Hidden Markov Model) و شبکه عصبی بازگشتی (Recurrent Neural Network) دو روش محبوب برای مدل‌سازی دنباله‌های زبانی هستند. تفاوت‌های اصلی بین این دو روش به شرح زیر هستند.

1. ساختار مدل

مدل پنهان مارکوف HMM: یک مدل آماری است که بر اساس فرضیه مارکوف دنباله‌ای از وضعیت‌های پنهان را مدل می‌کند که با توجه به آن مشاهده‌ها تولید می‌شوند. HMM شامل دو مجموعه اصلی از متغیرها است: متغیرهای پنهان (وضعیت‌های پنهان) و متغیرهای قابل مشاهده (مشاهدات). مدل پنهان مارکوف شامل ماتریس انتقال بین وضعیت‌های پنهان، ماتریس توزیع مشاهدات به شرط وضعیت‌های پنهان و بردار توزیع اولیه وضعیت‌های پنهان است.

شبکه عصبی بازگشتی RNN: به منظور مدل‌سازی دنباله‌ها و وابستگی‌های زمانی در داده‌ها طراحی شده است. در یک شبکه RNN، اطلاعات در طول زمان از طریق واحدهای بازگشتی (Recurrent Units) جریان می‌یابد. هر واحد بازگشتی دریافت ورودی مربوطه و وضعیت داخلی خود را به عنوان ورودی برای زمان بعدی دریافت می‌کند. واحدهای بازگشتی اجازه می‌دهند که شبکه اطلاعات قبلی را برای انجام کارها در آینده استفاده کند.

2. قابلیت مدل‌سازی

مدل پنهان مارکوف به خوبی برای مدل‌سازی دنباله‌هایی از وضعیت‌های پنهان و مشاهدات استفاده می‌شود. به عبارت دیگر، HMM قادر به برآورد وضعیت‌های پنهان مربوط به داده‌های مشاهده شده است.

شبکه عصبی بازگشتی به خوبی برای مدل‌سازی وابستگی‌های زمانی در داده‌ها و تحلیل دنباله‌ها مناسب است. با استفاده از واحدهای بازگشتی، RNN قادر به یادگیری و نگهداری اطلاعات در طول زمان است و می‌تواند الگوها و وابستگی‌هایزمانی را در داده‌ها تشخیص دهد.

3. یادگیری

یادگیری مدل پنهان مارکوف معمولا بر اساس الگوریتم Baum-Welch یا الگوریتم امتیاز خوشه‌بندی انجام می‌شود. این الگوریتم‌ها به صورت تکراری پارامترهای مدل را بهبود می‌بخشند تا توزیع احتمال بهتری برای وضعیت‌های پنهان و مشاهدات فراهم کنند.

فرآیند یادگیری در شبکه عصبی بازگشتی معمولا با استفاده از الگوریتم پس‌انتشار خطا (Backpropagation) و الگوریتم کاهش گرادیان (Gradient Descent) صورت می‌گیرد. این الگوریتم‌ها شبکه را قادر به بهینه‌سازی پارامترها بر اساس خطا ورودی-خروجی می‌کنند.

4. قابلیت مدل‌سازی دقیق

مدل پنهان مارکوف معمولا مناسب برای مدل‌سازی داده‌هایی است که فرضیه مارکوف را دنبال می‌کنند و وابستگی‌های طولانی در زمان را نمی‌توانند مدل کنند. این مدل به عنوان یک مدل زبانی نیز محدودیت‌هایی دارد و به طور معمول برای وظایف ساده‌تر مورد استفاده قرار می‌گیرد.

در شبکه عصبی بازگشتی با وجود واحدهای بازگشتی مدل وابستگی‌های طولانی در زمان را نگه می‌دارد. بنابراین، شبکه می‌تواند اطلاعات را به طول دنباله حفظ کند و وابستگی‌های طولانی‌تر را یاد بگیرد. به همین دلیل، شبکه عصبی بازگشتی معمولا برای وظایف پیچیده‌تر در حوزه پردازش زبان طبیعی مورد استفاده قرار می‌گیرد.

بخوانید: آشنایی با اصطلاحات مهم و رایج هوش مصنوعی (AI)